ICML21 Paper

Abstract

We introduce a novel loss function, Covariance Loss, which is conceptually equivalent to conditional neural processes (CNPs) and has a form of regularization so that it is applicable to many kinds of neural networks. Our covariance loss maps input variables to basis space by highly reflecting the dependencies of target variables as well as mean activation and mean dependencies of input and target variables. This nature enables the resulting neural networks to become more robust to noisy observations and recapture missing dependencies from prior information. We can see the application of covariance loss outperforms state-of-the-art models.

Covariance Loss

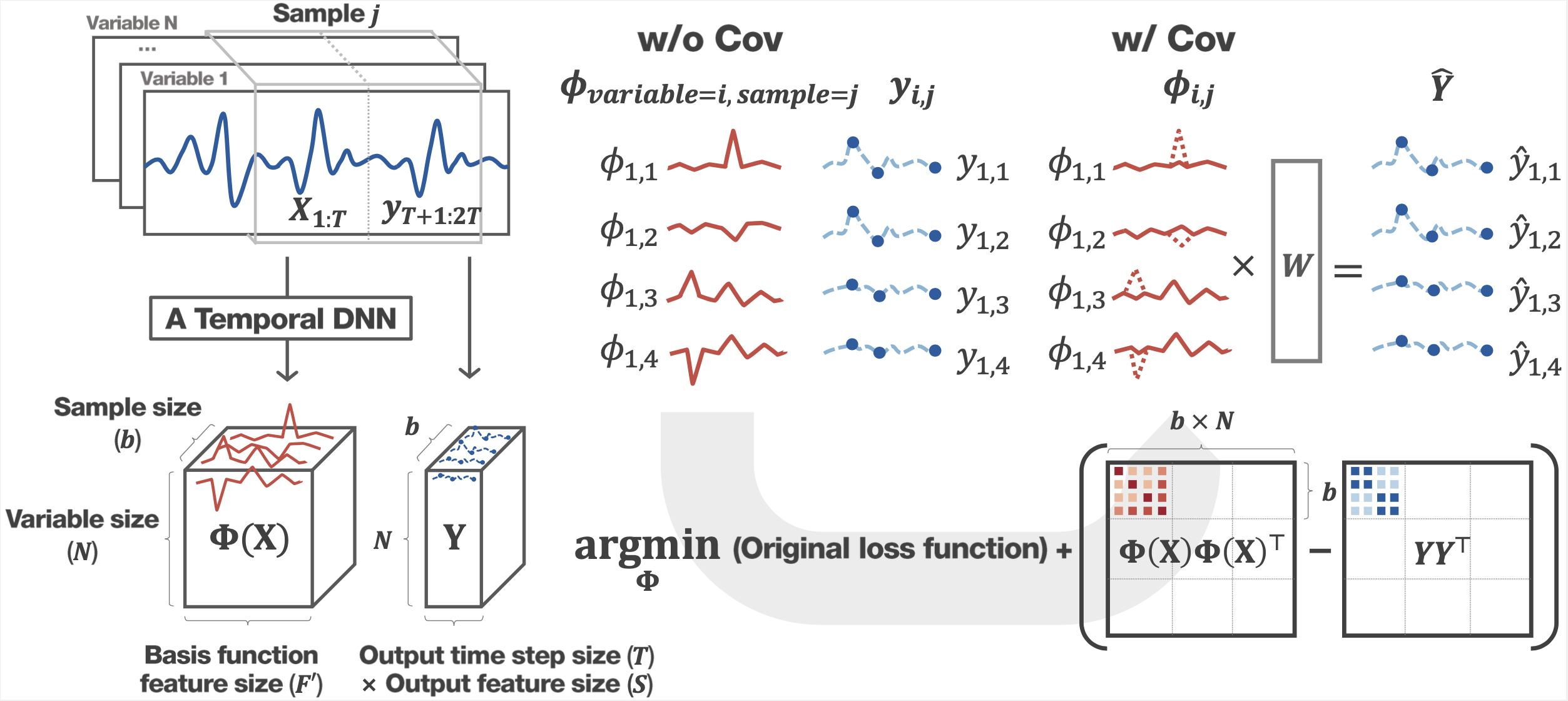
This figure shows the key idea of covariance loss. We learn a mapping function with a temporal deep neural network for a given dataset, for example, in our paper, we use Spatio-temporal graph convolutional networks (STGCN) and graph wavenet (GWNET). During the learning with covariance loss, we find a basis function space that minimizes not only the traditional mean square error of prediction but also the mean square error between covariance matrices of basis functions and target variables (this is our covariance loss term). The traditional way to optimization based on the mean square error usually results in finding a basis function space that only considers the mean activation of input variables and ignores the dependencies of target variables. Thus, for example, in cases the target variables are similar but input variables vary due to some kind of noisy signals, their basis functions may be irrelevant to each other, and incorrect predictions can be made as shown in the case ‘without cov’ in this image. In contrast, covariance loss forces basis functions to reflect dependencies of target variables so that the irrelevant basis functions become similar as well even though it sacrifices the mean activation as shown in case ‘with cov’ so that the results get the noisy robust prediction.

The Effect of Covariance Loss on Classification

To show the effect of covariance loss we analyze this on both classification and regression problems. First, we employ a simple deep neural network (DNN) for the classification and compare characteristics of resulting basis function spaces on the MNIST dataset. The following results of covariance matrices’ elements are sorted in ascending order of the labels (0 to 9).

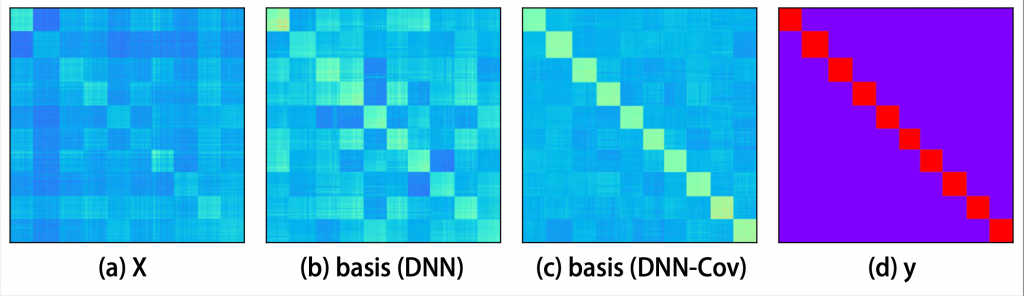
As shown in the above figure, the covariance matrices of the basis fuctions are computed from each model. The covarianc matrix from the DNN with covariance loss (c) has a similar pattern with the covariance matrix of the target variables (d) while the covariance matrix of the basis function generated by DNN (b) seems to have a similar pattern with that of input variables (a). We can see that the basis functions (b) for each sample are highly affected by mean activations of input variables (a) and thus, even though the samples belong to different classes. Meanwhile, the covariance loss (c) focuses more on finding a space in which only the basis functions which belong to the same class have high covariance while the basis functions for different classes have small covariance to reflect the dependencies of target variables.

We also analyze the ambiguous samples. The above sample (left) looks similar to the class ‘0’ and the prediction with mean activation of the input variable is incorrect (middle). In contrast, the optimization with covariance loss shows the correct prediction for the ambiguous sample (right).

The Effect of Covariance Loss on Regression

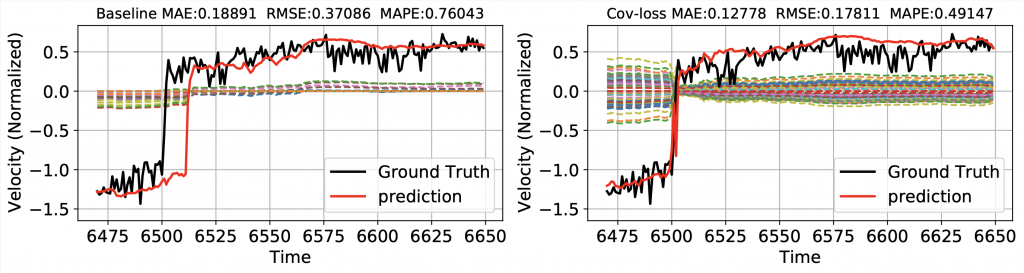
Next, we show the effect of the covariance loss on regression problems such as the traffic forecasting problems. As shown in the following figure, the predictions without covariance loss (red line) show qualitatively more competative predictions. More specifically, predictions from genuine GWNET (blue lines) are vulnerable to noisy nodes (left), and furthermore fail to detect the beginning of rush our (right). The optimization with covariance loss function (red line), however, not only achieve predictions more robust for noisy nodes but also successfully detect the rush hours.

Even though STGCN and GWNET can capture the underlying spatio-temporal dependencies automatically, still suffers from inaccurate predictions caused by noisy observations and misconnected dependencies. The above figure shows that the covariance loss may become a promising solution for such cases since it has a chance to discover the dependencies between every pair of target variables.

The above figures show the weighted basis functions, whose summation (at time t) is the prediction. In the case that a network optimized with Covariance Loss (right), we can see dashed lines have similar patterns with predictions and the end of rush hour is successfully detected. This is mainly due to the consideration of the dependencies of target variables. In our paper, we analyze the constraint imposed by the consideration and show the effect of covariance loss with extensive sets of experiments.

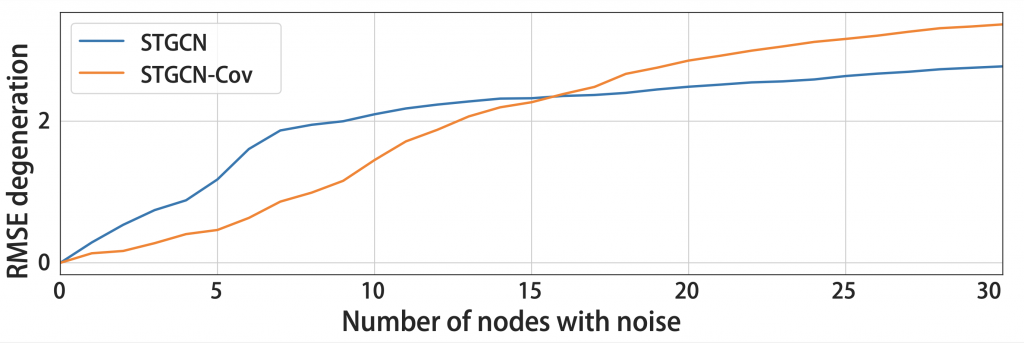
Noise Robustness

We also analyze the robustness of covariance loss on noisy observations. As in the following figure, as the number of noisy nodes increases, the performance of a regression model with covariance loss increases slower than the same regression model without covariance loss until 15 noisy nodes. This is because the model with covariance loss follows global dependencies at a higher number of noisy nodes than 15.

Scalability

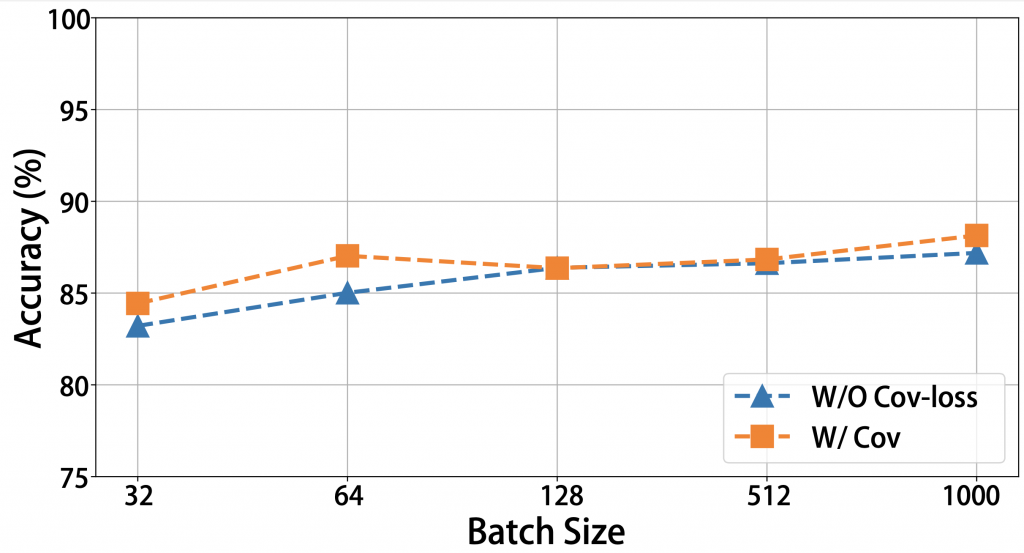
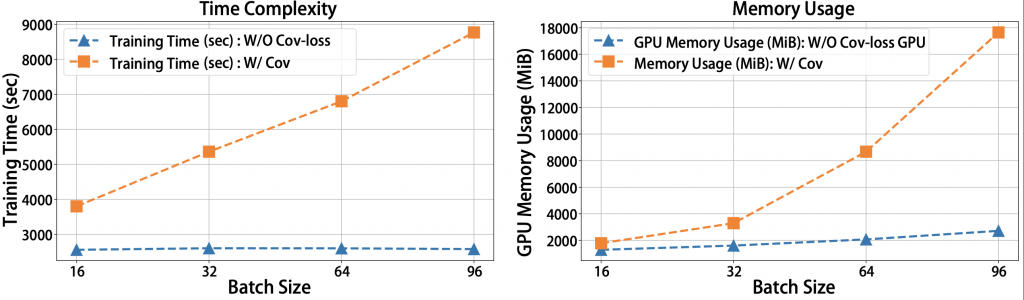
Since we employ a mini-batch dataset-based learning scheme with many iterations, we evaluate the effect of batch size on accuracy and time complexity. We compare classification accuracy on the CIFAR10 dataset by varying batch size to identify the scalability of batch size as shown in the following figure. We can see that the effect of batch size is not significant. This is because, under the random batch-based training scheme with many iterations, mini-batch-based covariance loss evaluation is eventually converged to the Gram matrix \( \mathbf{K} \) based evaluation.

We also test the required memory usage and running time with increasing batch size in the following figure. Since the random mini-batch sampling scheme, it is applicable to larger datasets. However, memory requirements and running time are proportional to the batch size.

Contribution

We propose a novel loss function, covariance loss, that is applicable to several kinds of neural networks with a simple modification to the existing loss. Optimization with covariance loss enables neural network models to learn basis function space which explicitly reflects the inter and intra dependencies of target variables, This is the main reason for the success of GPs and CNPs. However, while GPs and CNPs find the empirical covariance as the solution of the maximum likelihood \(\textbf{K} = \widetilde{\mathbf{\Sigma}}_\textbf{y} \), covariance loss works as a constraint to find basis space which is directly reflected the relationship between target variables

Publication

ICML 2021 (Proceedings of the 38th International Conference on Machine Learning, PMLR 139, 2021)